Kara delikler hakkındaki teorik sonuçlar, evrenin devasa bir hologram olabileceğini göstermekte! 
Fiziksel dünyanın neden meydana geldiğini herhangi bir kişiye sorduğunuzda, vereceği cevap muhtemelen: “madde ve enerji”den şeklinde olacaktır.
Mühedislikten, biyolojiden ya da fizikten öğrendiğimiz bir şey varsa o da; “bilgi”nin çok önemli bir içerik olduğudur. Otomobil fabrikasıdaki robota, metal ve plastik tedarik edilse de hangi kısmın, hangi kısım ile birleştirileceğine yönelik önemli ve gerekli bilgiye sahip olmadan o robot işe yaramaz. Bedeninizdeki hücre içindeki ribozom amino asid yapı taşlarıyla doludur ve ATP’nin ADY’ye çevrilmesiyle açığa çıkan enerji ile güçlenir. Ancak, hücre çekirdeği içindeki DNA’dan gelen bilgiler olmadan hiç bir proteini sentezleyemez. Aynı şekilde bir yüzyıl içinde fizikteki gelişmeler, bize “bilgi”nin fiziksel sistemler ve prosesler için çok önem teşkil ettiğini öğretmiştir ve hattâ Princeton Üniversitesi’nden John A. Wheeler’in başlattığı ve güncel eğilim şudur: fiziksel dünyanın enerji ve maddenin de içeriği olan ve onlardan daha önemli olan bilgiden meydana geldiği.
Bu bakış açısı eski ve önemli sorulara yeni bir bakış açısı getiriyor. Sabit disk sürücüler gibi cihazların bilgi depolama kapasitesi hızla artmaktadır. Bu işlem-ilerleme ne zaman duracak? Diyelim bir gramdan az ağırlığa sahip olan ve bir santimetre küp içine (kabaca bilgisayar çipinin boyutu) sığabilecek bir cihazın nihai bilgi kapasitesi ne olabilir? Tüm bu evreni tanımlamak için ne kadar bilgi gerekir?, bu tanımlama bir bilgisayarın hafızasına sığar mı? William Blake’in unutulmaz sözü olan “ Bir kum tanesinde tüm dünyayı görürsün” dediği şekilde görebilir miyiz yoksa bu anlatım sadece şiirsel bir anlatımdan öteye gitmeyen bir şey midir?
Dikkat çekici bir şekilde, teorik fizikteki son gelişmeler bu soruların bazılarını yanıtlamakta ve cevaplar nihai “gerçeklik teorisi” için önemli ipuçları verebilmektedir. Fizikçiler, kara deliklerin gizemli özelliklerini inceleyerek, uzayın bir kısmında ya da maddenin veya enerjinin niceliği konusunda ne kadar çok bilgiye sahip olunabileceğinin mutlak sınırları konusunda bir çıkarım yaptılar. Bu konuya dair sonuçlar, üç boyutlu algıladığımız evrenimizin, bir “hologram”şeklinde “iki boyut”lu bir yüzey üzerine “yazılı” olabileceğini ortaya koymakta. O zaman, dünyayı üç boyutlu olarak gördüğümüz günlük algılarımız ya çok derin bir “illüzyon” ya da ya da gerçekliğe bakmanın iki alternatif yolundan sadece bir tanesi… Bir kum tanesi dünyamızı kapsamayabilir ama düz bir ekran kapsayabilir.
İki Entropi Masalı

FORMAL BİLGİ TEORİSİ (BİLGİ KURAMI) nın temelleri Amerikalı uygulamalı matematikçi olan Claude E. Shannon’ın “ İletişimin Matematiksel Teorisi” adlı makalesi ile ilk olarak ortaya konulmuştur. Bu teoride Shannon, bugün bilgiyi ölçmede en geniş çapta kullanılan kavram olan “entropi”yi bizlere sunmuştur. Entropi, uzun süre ısı ile ilgilenen fizik dalı olan termodinamiğin ana, kavramı olmuştur. Termodinamik entropi, fizik sistemindeki bir bozukluk şeklinde yaygın olarak tarif edilir. 1877’de Avusturyalı fizikçi Ludwig Boltzmann, entropinin, maddenin parçalarını oluşturan parçacıkların, maddenin makroskopik parçaları ile aynı gözükürken bulunabilecek farklı mikroskobik durumların sayısını daha belirgin bir şekilde gösteren özelliğini ortaya koyar. Örneğin; odada etrafınızdaki havada bulunan gaz moleküllerinin tüm dağılım yollarını ve olası hareket şekillerinin sayabilirsiniz..
Shannon, bilginin içeriğini nicelendirmek için örneğin; mesaj gibi, bir yol bulurken, Boltzmann mantığıyla aynı formda olan bir formüle yönelir. Shannon entropisinin mesajı, onu kodlamak için gerekli iki basamaklı sayılardan ya da “bit”lerden meydana gelmektedir. Shannon’un entropisi, oldukça yüksek bir şekilde içeriğe bağlı olan bilginin değeri hakkında bizi aydınlatmamaktadır. Ancak yine de bilginin objektif ölçümü olarak, onun sunduğu entropi, bilim ve teknolojide son derecede yararlı olmuştur. Örneğin; cep telefonlarından modemler, modemlerden kompakt disklere kadar her modern iletişim cihazının tasarımı Shannon entropisine dayanır.
Termodinamik entropi ve Shannon entropisi kavramsal olarak eşdeğerdir: Boltzmann entropisi tarafından sayılan düzenlemelerin sayısı, herhangi bir özel düzenlemeyi uygulamak için gereken “Shannon bilgileri”nin miktarını yansıtmaktadır. Ancak bu iki entropinin iki belirgin farklılığı vardır: İlk olarak, bir kimyager veya soğutma mühendisi tarafından kullanılan termodinamik entropi, ısı olarak bölünen enerji birimleri cinsinden kullanılırken, bir iletişim mühendisinin kullandığı Shannon entropisi, esasen boyutsuz, “bit”ler halindedir. Bu fark, sadece bir konvansiyon meselesidir.
Bununla birlikte, ortak ünitelere indirgendiğinde bile, iki entropinin tipik değerleri büyük oranda farklılık gösterir. Örneğin; bir gigabayt veri taşıyan silikonlu bir mikroçip, oda sıcaklığında yaklaşık 1023 bit olan yonganın termodinamik entropisine göre çok daha küçük olan yaklaşık 1010 bitlik bir Shannon entropisini (bir bayt sekiz bit) içerir. Bu tutarsızlık, entropilerin farklı serbestlik derecelerinin hesaplanmasından dolayı oluşur. Bir serbestlik derecesi, bir parçacığın yerini veya hızının bir bileşeni gibi değişebilen herhangi bir miktardır. Shannon entropi çipi, yalnızca silikon bir kristalin içine işlenmiş her minik transistörün genel durumuyla ilgilidir. (transistor açık ya da kapalı; 0 veya 1–tek bir ikili serbestlik derecesi–. )
Buna karşın, termodinamik entropi, her transistörü oluşturan milyarlarca atomun (ve onların dolaşım elektronlarının) durumuna bağlıdır. Minyatürleşme, her atomun bizim için bir bit bilgi depolayacağı güne yaklaşırken, en gelişmiş mikroçipiyle kullanışlı Shannon entropisi de maddenin termodinamik entropisinin sınırlarına büyük ölçüde yaklaşacaktır. Bu iki entropi, aynı serbestlik dereceleri için hesaplandığında eşittirler.
Peki, nihai serbestlik dereceleri nedir?… Herşeyden önce atomlar, elektron ve çekirdeklerden oluşurlar, çekirdekler de proton ve nötron kümeleşmesinden, maddenin temel parçacığı ve bileşeni olduğu varsayılan süpersicim uyarımları olan quarklardan oluşur. Ancak fizikteki bu bir asırlık vahiylerin değişimi, bizleri dogmatik olmamamız konusunda uyarmakta… Evrende günümüz fiziğinde hayâl edilebilenden daha fazla yapı seviyeleri olabilir!
Bir madde kütlesinin nihai bilgi kapasitesini veya eş değer olarak, onun gerçek termodinamik entropisini, (X seviyesi olarak adlandıracağımız) maddenin nihai bileşenlerinin veya en derin yapı seviyelerinin doğasını bilmeden hesaplanamaz.( Bu belirsizlik arabaların motorlarında olduğu gibi pratik termodinamik analizlerde herhangi bir problem oluşturmaz.Çünkü, motorda nispeten yararlı koşullar altında durumlarını değiştirmez.) Minyatürleşmedeki başdöndürücü ilerleyişi göz önüne aldığımızda, quarkların bilgiyi (belki bir bit- bir parça) depolamaya hizmet edeceği günün geleceğini düşünebiliriz.
Peki o zaman bir santimetre küpünüze ne kadar fazla bilgi sığabilir? Ve süpersicimleri ya da daha derininden, hiç hayal bile edemeğimiz boyutlardan yararlansak, ne olurdu?… Şaşırtıcı bir şekilde, son 30 yıldaki yerçekimi fiziğindeki gelişmeler, cevaplaması zor görülen sorulara bazı net cevaplar sağlamıştır.
Kara Delik Termodinamiği
Bu gelişmelerin ana oyucusu karadeliktir. Karadelikler, 1915 Albert Einstein’ın çekim gücünün geometrik teorisi, genel göreliliğin bir sonucudur. Bu teoride, çekim, nesneleri bir kuvvet tarafından çekilmiş gibi hareket ettiren uzay-zamanın eğriselliğinden ortaya çıkar. Tersine eğrisellik, maddenin ve nerjinin varlığından kaynaklanır. Einstein’ın denklemlerine göre, yeterince yoğun bir madde veya enerji konsantrasyonu, uzay-zamanı öylesine büker ki, bu karadeliğin oluşmasına neden olur. Klasik fiziğin (Kuantum olmayan) tanımında görelilik kanununa göre,karadeliğe düşen herhangi birşey tekrar dışarı çıkamaz. Olay ufku olarak tanımlanan dönüşü olmayan nokta çok önemlidir. En basit durumda,ufuk, yüzey alanı daha büyük karadelikler için daha geniş ve büyük olan bir küredir.
Bir karadeliğin içinde ne olduğunu belirlemek olanaksızıdr. Ufuktan herhangi detaylı bir bilgi dış dünyaya çıkamaz. Ancak, karadeğilin içinde sonsuza kadar kaybolan bir parça madde bazı izler bırakır. Onun enerjisini( herhangi bir kütleyi enerji olarak Einstein’ın E = mc2) Einstein’ınkine göre saydığımızda kalıcı olarak karadeliğin kütlesi içinde aratan bir şekilde yansır. Madde delik etrafında dönerken yakalanırsa, ilgili açısal momentumu karadeliğin açısal momentumuna eklenir. Bir karadeliğin hem kütlesi, hem de açısal momentumu, deliğin uzay-zamandaki etkilerinden ölçülebilir. Termodinamiğin ikinci kanunu da burada ihlal edilmiş gözükmektedir…
Termodinamiğin ikinci kanunu, doğadaki çoğu işlemin geri döndürülmez olduğu, tanıdık bir gözlemi özetler: Bir çay fincanı masadan düşer ve parçalanır. Ancak hiç kimse parçaların kendiliğinden bir araya gelip de yeniden birleşerek bir çay fincanı olduğunu görmemiştir. Termodinamiğin ikinci kanunu bu şekildeki tersine işlemleri yasaklar. Bu kanuna göre, izole edilmiş fiziksel bir sistem hiç bir zaman azalamaz; en iyi durumda entropi sabit kalır ve genellikle de artar.
Bu kanun fiziksel kimya ve mühendisliğin merkezidir ve fiziğin dışındadır, ancak fizik (fizik kanunu olduğu tartışmalı bile olsa) üzerinde büyük etkisi olan bir kanundur.
İlk olarak Wheeler’ın üzerinde durduğu gibi; bir nesne kara deliğin içinde kaybolduğu zaman, onun entropisi tamamen yok olur, ve böylece termodinamiğin ikinci kanunu da geçersiz gözükür. Bu bilmeceyi çözmedeki ilk ipucu, 1970 yılında ortaya çıkar. O dönemde Demetrious Christodoulou (Princeton Üniversitesi’nde Wheeler’ın yüksek lisans öğrencisi) ve Cambridge Üniversitesi’nden Stephen W. Hawking birbirlerinden bağımsız olarak çeşitli proseslerde örneğin; kara delik birleşmelerinde olduğu gibi olay ufuklarında hiç bir şekilde bir azalma olmadığını ispatlarlar. Entropinin artması ile ilgili olarak yapılan analoji, benim 1972 yılında şu öneriyi getirmeme sebep olur: ‘’Kara deliğin entropisi onun ufku ile orantılıdır.”
Benim düşünceme göre; kara deliğin içine bir madde düştüğünde, kara deliğin entropisindeki artış her zaman bu maddenin kaybettiği entropiyi tamamlar, ve hattâ gereğinden fazla tamamlar. Daha genel olarak, kara delik entropilerinin toplamı ve de kara deliklerin dışındaki entropiler azalamaz. Kısaca; bu “genelleştirilmiş” ikinci kanundur (GSL). Bu genelleştirilmiş ikinci kanun (GSL) tamamen teorik olan, çok sıkı testlerden geçmiştir.
Bir yıldız kara delik oluşturmak üzere çöktüğü zaman, kara deliğin entropisi yıldızın entropisinin çok üzerindedir.1974 yılında Hawking, kara deliğin spontane şekilde termal radyasyon yaydığını, bir kuantum işlemi ile (Hawking Radyasyonu olarak bilinen işlem) uygulamalı olarak göstermiştir. (‘’The Quantum Mechanics of Black Holes’’, Stephen Hawking, Scientific American, January 1977)
Bu fenomen (kara deliğin kütlesi ve buna bağlı olarak ufuk alanının azalmakta olması) karşısında Christodoulou-Hawking teoremi geçersiz kalır.
Ancak,Genelleştirilmiş İkinci Kanun (GSL) bununla başa çıkar: yayılan radyasyonun entropisi, kara deliğin dekrementi içindeki entropiyi tamamlamaktan çok daha fazlasını yapar, böylece genelleştirilmiş ikinci kanun (GSL) korunmuş olur. Karadeliklerin maruz kalacağı herhangi olası bir işlem için GSL’nin geçerli olduğunu göstermek için, 1986’da Syracuse Üniversitesi’nden Rafael D. Sorkin, ufuğun rolünü-işlevini kullanarak, dışardaki etkileyici olaylardan kara deliğin içindeki bilginin, etkilemesini engellemiştir. Böylece, GSL veya ona benzeyen başka bir şey, kara deliklerin geçirdiği inandırıcı işlem aşamaları için çok geçerlidir.
Onu bu çok derin argumanı, GSL’ye giren entropinin, hangi seviyede olursa olsun, X seviyesine kadar hesaplandığını açıkça ortaya koyar.
Hawking’in radyasyon prosesi, onun kara delik entropisi ile ufuk entropisi arasındaki sabit değeri belirlemesini sağlamıştır. Planck alanlarına göre (Planck uzunluğu 10–33cm kadardır ve yerçekimi ve kuantum mekaniği ile ilgili en temel ölçüdür. Planck alanı ise bu uzunluğun karesidir.) ölçülen ufuk alanının dörtte biri, kara deliğin entropisidir. Termodinamik olarak bile bu, çok büyük bir entropi miktarıdır. Bir santimetre çapındaki bir kara deliğin entropisi 1066 bit tir, ki bu tek kenarı 10 milyar kilometre olan bir küp suyun entropisine eşittir.
Hologram Olarak Dünya
Genelleştirilmiş ikinci kanun (GSL), izole edilmiş herhangi bir fizik sistemine sınırlar koymamızı sağlar. Bu sınırlar ‘’X’’ seviyesine kadarki tüm seviyelerdeki yapılardaki bilgiyi kapsar. 1980’de ben, evrensel entropi sınırı olarak tanımlanan bu sınırların birincisi üzerinde çalışmaya başladım. Bu sınır, ölçüsü belirlenmiş bir kütlenin ne kadar entropi taşıyabileceğini belirler. Bununla alakalı olan “holografik” sınır fikri, Stanford Üniversitesi’nden Leonard Süsskind tarafından ortaya atılmıştır. Bu sınır da uzayda belirli bir hacim kaplayan madde ve enerjinin ne kadar entropi taşıyacağını belirler. Holografik sınır ile ilgili çalışmasında Susskind, kara delik olmayan, ancak küre şeklinde, izole edilmiş ve ‘’A’’ olarak tanımlanan, kapalı bir alanın içinde yerleşik olan bir kütleyi incelemiştir.
Kütle çöküp bir kara delik haline dönüşürse, bu delik “A’’ dan daha küçük bir ufuk alanı ile sonuçlanacaktır. Dolayısıyla, kara deliğin entropisi A/4’ ten daha küçüktür. Genelleştirmiş İkinci Kanuna göre, sistemin entropisi azalamaz, bu nedenle kütlenin orijinal entropisi A⁄ 4 ‘ten daha büyük olamaz. Sonuç olarak, sınırı A alanı ile izole edilmiş bir fiziksel sistemin entropisi A⁄ 4’ten daha küçük’tür. Kütle aniden ve kendiliğinden çökmezse ne olur?… Ben, 2000’de Susskind’in argümanından çok farklı olmayan bir argüman ortaya koydum: Küçük bir kara delik kullanılarak, bütün sistem kara deliğe dönüşebilirdi. Dolayısıyla, sınır, sistemlerin ana yapısından veya X düzeyi doğasından bağımsızdır. Sadece Genelleştirilmiş İkinci Kanuna bağlıdır. Biz, şimdi artık bilgi depolanmasının maksimum limitleri hakkındaki soruları cevaplandırabiliriz. Bir santimetreyi ölçen bir alet, prensip olarak 1066 bite kadar bilgi tutabilir. Bu akıllara durgunluk veren bir miktardır. Görünür evren en azından 10100 bit’lik entropi içerir. Prensip olarak bu miktar, çapı bir ışık yılının onda biri olan bir kürenin içine yerleştirilebilir. Evrenin entropisini hesaplamak zor bir problemdir, ancak evrenin kendi büyüklüğünde bir küreye gereksinme gösteren çok daha büyük sayıların da ortaya çıkması mümkündür.

Ancak, esas şaşırtıcı olan, holografik sınırın diğer bir özelliğidir.
Kısacası, mümkün olan maksimum entropi hacim yerine sınırlayıcı alana bağlı olmasıdır. Bilgisayarın hafıza chiplerini toplayıp, büyük bir yığın haline getirdiğimizi bir düşünün… Transistörlerin sayısı (toplam veri depolama kapasitesi) bu yığın hacmi ile orantılı olarak artar. Böylece, tüm çiplerin toplam termodinamik entropisi de artış gösterir. Dikkâti çeken bir diğer nokta da; teorik olarak, yığının kapladığı alanın bilgi kapasitesi, sadece yüzey alanına bağlı olarak artmaktadır. Hacim, yüzey alanından daha hızlı yükseldiği için, belli bir noktaya gelince, tüm çiplerin tamamının entropisi holografik sınırı aşacaktır.
Bu durumda ya Genelleştirilmiş İkinci Kanunun (GSL) ya da bizim entropi ile ilgili sağduyuya dayalı fikirlerimizin geçersiz olması gerekmektedir. Aslında geçersiz olan; yığının kendisidir, çünkü bu engeli aşmadan önce kendi çekiminin altında çöker ve bir kara delik oluşturur. Bundan sonra da her ek çip, kara deliğin kütlesini ve yüzey alanını Genelleştirilmiş İkinci Kanunu koruyacak şekilde arttar.
“Bilgi kapasitesinin yüzey alanına bağlı olduğu”na dair bu şaşırtıcı sonuç—1993 yılında Hollanda’nın Utrecht Üniversitesi’nden Nobelist Gerard ‘t Hooft tarafından önerilen ve Susskind tarafından hazırlanan “holografik ilke”nin doğru olduğu takdirde—, doğal bir açıklamayı da beraberinde getirmekte.
Günlük yaşamda bilinen bir “hologram”, doğru şekilde aydınlandığında, tam bir üç boyutlu görüntü oluşturan özel bir fotoğraf türüdür. Bu Üç Boyutlu görüntüyü tanımlayan tüm bilgiler, yeniden oluşturulmaya, şekil almaya hazır olan iki boyutlu bir film parçasının üzerindeki açık ve koyu renkli desenlerin üzerine kodlanmıştır.
Holografik prensip, bu görsel büyünün benzerinin, üç boyutlu bir yer kaplayan herhangi bir sistemi fiziksel olarak tanımlamak için uygulanabilir olduğunu ileri sürer: bu prensibe göre, başka bir fizik teorisi sadece iki boyutlu bölgenin sınırının üzerinde tanımlanmasına rağmen, tamamen üç boyutlu fiziği tanımlayabilir. 3 Boyutlu bir sistem, sadece 2 boyutlu sınırıyla çalışan bir fizik teorisi ile tam olarak tanımlanabiliyorsa, o zaman sistemin bilgi içeriğinin sınırdaki tanımlamayı aşmaması düşünülür..
Sınırı Üzerine Resmedilmiş Bir Evren
Biz holografik prensibi bütün evrene uygulayabilir miyiz?… Aslında evren 4 Boyutlu bir sistemdir, hacmi vardır ve zamanla genişler. Eğer bizim evrenimizin fiziği “holografik” ise, o zaman alternatif bir takım fizik kanunları da olacaktır ve bu kanunlar bir yerlerde uzay-zamanın 3 Boyutlu sınırı üzere çalışacaktır ve bu bildiğimiz 4 Boyutlu fiziğe eş değer olacaktır. Şu anda henüz bu şekilde çalışan bir 3 boyutlu teori bilmiyoruz. Gerçekte evrenin sınırı olarak hangi yüzeyi kullanmamız gerekir? Bu fikirleri gerçekleştirebilmek için atılacak ileri bir adımsa; evrenimize dair daha basit modelleri incelemek olabilir.
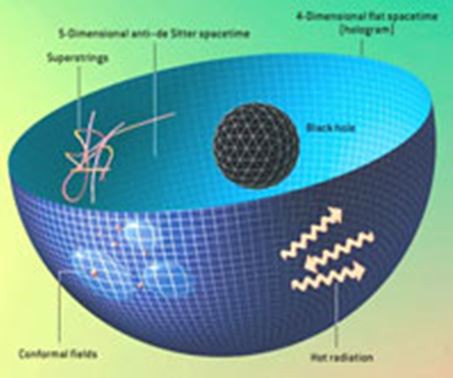
Holografik prensiple ilgili somut örnekler, anti-de Sitter uzay zamanlarını içerir. Orijinal “de Sitter, uzay-zamanı ve kozmolojik sabit” olarak bilinen itici güç ile birlikte ilk defa Hollandalı astronom Willem de Sitter tarafından 1917 yılında Einstein’ın denklemlerine bir çözüm olması amacı ile ortaya konmuştur. De Sitter’in uzay-zamanı boştur ve gittikçe ivmesi artan bir şekilde genişlemektedir ve çok yüksek bir simetrisi vardır.1997’de uzaktaki süpernova patlamalarını inceleyen astronomlar, evrenimizin ivmesinin gittikçe artan bir şekilde genişlediğini ve gelecekte büyük bir olasılıkla da “Sitter uzay-zaman”ı gibi olacağı sonucuna varmışlardır.
Şimdi, eğer Einstein’ın denklemlerindeki tekrarlama çekim gücüne dönüşürse; de Sitter’in çözümü eşit derecede bir simetri olan anti-de Sitter uzay-zamanına dönüşür. Holografik konsept için daha da önemli olan nokta ise; bu uzay zamanın bir sınırının olması ve bu sınırın da ‘’sonsuzluk’’ta konumlanmasıdır ve bu, bizim günlük uzay-zamanımıza çok benzeyen bir sınıra sahiptir.
Teorisyenler, anti-de Sitter uzay-zamanını kullanarak, holografik ilkeye somut bir örnek oluşturmuşladır. Anti-de Sitter uzayında çalışan süper sicim teorisi ile tanımlanan evren, sınırın üzerinde çalışan bir kuantum alan teorisine tamamen eş değerdir. Böylece, bir anti-de Sitter evrenindeki süper sicim teorisi evrenin sınırına resmedilmektedir.
1997’de Harvard Üniversitesi’nden Juan Maldacena, 5D anti-de Sitter olayı ile ilgili öyle bir ilişki olduğunu ileri sürer. Daha sonra bu, Princeton, İleri Çalışmalar Enstitüsüne mensup Edward Witten ve aynı Üniversitesi’nden Steven S.Gubser, Igor R. Klebanov ve Alexander M.Polyakov tarafından da onaylanır. Bu holografik iletişimin örnekleri şimdi çok değişik boyutlardaki uzay zamanlar için de bilinmektedir. Bu sonuç göstermektedir ki; çok farklı görünen iki teori aynı boyutun uzayında çalışmasalar bile birbirine eşdeğerdedir. Bu evrenlerin herhangi birinde yaşayan canlılar, string teori süpersicim tarafından tanımlanan 5 Boyutlu bir evrende mi, yoksa nokta parçacıkların kuantum alan teorisi ile tanımlanan 4 Boyutlu bir evrende mi yaşadıklarını tesbit edemeyeceklerdir. Çünkü, onların beyin yapıları önyargıya dayalı hüküm verecektir. Bu önyargıya göre de tanımlardan birisini geçerli olarak kabul edeceklerdir, tıpkı bizim beyinlerimizin evrenimizin Üç Boyutlu olduğuna dair sahip olduğumuz algılamada olduğu gibi…
Holografik eşdeğerlilik, 4 Boyutlu uzay-zamanda zor bir hesap işlemine yol açar, çünkü, kuark ve gluonların davranışları ve bunların birbirleri ile etkileşimleri söz konusudur. Ancak, çok simetrik olan 5 Boyutlu anti-de-Sitter uzay-zamanda bu hesap daha kolaydır. Bu eşdeğerlilik diğer yönden de işler. Witten, anti-de Sitter uzay-zamanında kara deliğin, sınırlayıcı uzay süresinde çalışan alternatif fizikte sıcak radyasyona karşılık geldiğini göstermiştir. Deliğin entropisi (son derece derin ve akıllı bir kavram) radyasyonun entropisine eşittir ve bu çok sıradan, normaldir.
Genişleyen Evren
Yüksek oranda simetrik ve boş olan
5 Boyutlu anti-de Sitter evreni, 4 Boyutlu olan, madde, radyasyon,ve pek çok zarar verici şiddet dolu olaylara sahip olan evrenimize benzemez. Biz kendi evrenimizi, içinde madde ve düzgün bir şekilde yayılmış radyasyonu olan bir evren gibi düşünsek de yine de bir anti-de-Sitter evreni elde edemeyiz ve de daha çok ‘’Friedmann-Robertson-Walker’’ evreni elde ederiz. Bugün pek çok kozmolog evrenimizin bir Friedmann-Robertson-Walker evrenine benzediği konusunda fikir birliğine varmıştır: “Sonsuz, sınırı yoktur ve sonsuza kadar genişlemeye devam edecektir.”
Böyle bir evrenin holografik ilkeyle veya holografik sınırla uyumu var mı? Susskind’in çökerek kara deliğe dönüşme ile ilgili argümanı burada bize yardımcı olamaz. Aslında, kara deliklerden ortaya çıkan; holografik sınırın düzenli bir şekilde genişleyen evrende kırılması gerektiğidir. Eşit bir şekilde madde ve radyasyonla dolu olan bir bölgenin entropisi hacmi ile orantılıdır. Dolayısıyla, yeterince geniş bir bölge holografik sınırları ihlal edecek, geçersiz kılacaktır.
1999’da Stanford Üniversitesi’nden Rafael Bousso, modifiye edilmiş bir holografi sınırı önermiş ve o günden beri bunun, daha evvel tartıştığımız sınırların uygulanamadığı yerlerde bile, uygulandığı görülmüştür. Bousso’nun formülü herhangi uygun bir 2 Boyutlu yüzeyle başlar, bu yüzey bir küre gibi kapanabilir veya bir sayfa gibi açılabilir. Burada yüzeyin tek kenarından aynı anda ve dikey olarak çıkan ışık patlamaları düşünülür. Talep edilen tek şey, başlangıç için aynı noktaya gelen hayali ışık ışınlarıdır. Örneğin; küre şeklinde bir kabuğun iç yüzeyinden gelen ışık bu gereksinimi karşılar. Daha sonra bu hayali ışık hüzmelerinin kesişmeye başladıkları noktaya kadar içinden geçtikleri madde ve radyasyonun entropisinin ne olduğu düşünülür. Bousso’nun düşüncesine göre bu entropi esas ana yüzeyin temsil ettiği entropiden daha fazla olamaz (Planck alanı birimine göre ölçüldüğü zaman ilk alanın dörtte biri kadar).Bu entropi hesaplaması, holografik sınırda kullanılan entropi hesaplama metodundan daha farklıdır. Bousso’nun sınırı, bir yerdeki belli bir zamandaki entropiyi anlatmamaktadır. Onun anlattığı şey; değişik zamanlardaki ve yüzeyden fışkıran ışıkla ‘’aydınlanan’’ yerlerdeki entropidir.
Bousso’nun sınırı, onların kısıtlamalarından uzak durarak,diğer entropi sınırlarını da kendisine katar.
Hem evrensel entropi, hem de Gerard‘t Hooft-Susskind formundaki holografik sınıra, Bousson’un holografik sınırından ulaşılabilir. Bousson’un sınırı çok hızlı gelişmeyen ve çekim alanı çok kuvvetli olmayan herhangi bir izole sistem için de geçerlidir. Eğer, bu şartlar aşılırsa, kara deliğin içine çöken madde küresinde olduğu gibi, o zaman bu sınırlar geçersiz olur, fakat Bousson’un sınırı geçerliliğini korur. Bousso stratejisi, üzerlerine dünya hologramları kurulabilecek 2 Boyutlu yüzeylerin yerlerini tespit etmek içinde kullanılabileceğini göstermiştir.
Bir Devrimin İşaretleri

Araştırmacalar, daha pek çok entropi sınırı önermişlerdir. Holografik motif üzerindeki varyasyonların hızla artmasının bu konunun henüz bir fizik kanunu olma durumuna gelmediğini göstermektedir. Ancak, holografik düşünce şekli tam olarak anlaşılmamış olmasına rağmen, bu noktanın üzerinde de epey durulacak gözükmektedir ve 50 yıldır geçerli olan “alan teorisi”nin, fiziğin tek ve temel dili olduğu görüşünden de vazgeçilmesi gerektiği idrak edilmiştir. Alanlar, örneğin; elektromanyetik alanlar bir noktadan diğerine değişim gösterir ve serbestlik derecelerinin sonsuzluğunu tanımlarlar. Süper sicim teorisi sonsuz sayıdaki serbestlik derecelerini içerir.
Holografi, sınırlanmış bir alan içinde mevcut serbestlik derecelerini sonlu bir sayıya indirger; sonsuzluğu ile birlikte alan teorisi hikayenin sonu değildir. Sonsuzluk kanıksansa bile, yüzey alan bilgisinin esrarengiz bağımlılığı mutlaka bir şekilde kalıcı olacaktır.
Holografi daha iyi bir teoriye rehber olabilir. Temel teori neye benzer? Holografiye bağlı olarak gelişen düşünceler zinciri, bazı kişilere örneğin; Waterloo’daki Perimeter Institute for Theoretical Physics adlı Enstitü’de çalışan Lee Smolin’e, şu fikri aşılamıştır: Bu son teoride alanlarla ve hatta uzay-zamanla değil, onun yerine daha çok fiziksel işlemler arasındaki bilgi değişimi ile ilgilenilmedir. Eğer bu böyle olursa, “dünyanın bilgiden meydana geldiği”ne dair olan görüş daha sağlıklı bir zemine oturacaktır.
Çeviren: AylinER
Scientific American Dergisi Ağustos 2003 sayısı’dan (52-83 sayfaları arası) çevrilmiştir.
 Okyanusum.com Din, Bilim, Sufizm
Okyanusum.com Din, Bilim, Sufizm



